Abstract

Capturing high-dimensional social interactions and feasible futures is essential for predicting trajectories. To address this complex nature, several attempts have been devoted to reducing the dimensionality of the output variables via parametric curve fitting such as the Bézier curve and B-spline function. However, these functions, which originate in computer graphics fields, are not suitable to account for socially acceptable human dynamics. In this paper, we present EigenTrajectory (𝔼𝕋), a trajectory prediction approach that uses a novel trajectory descriptor to form a compact space, known here as 𝔼𝕋 space, in place of Euclidean space, for representing pedestrian movements. We first reduce the complexity of the trajectory descriptor via a low-rank approximation. We transform the pedestrians' history paths into our 𝔼𝕋 space represented by spatio-temporal principle components, and feed them into off-the-shelf trajectory forecasting models. The inputs and outputs of the models as well as social interactions are all gathered and aggregated in the corresponding 𝔼𝕋 space. Lastly, we propose a trajectory anchor-based refinement method to cover all possible futures in the proposed 𝔼𝕋 space. Extensive experiments demonstrate that our EigenTrajectory predictor can significantly improve both the prediction accuracy and reliability of existing trajectory forecasting models on public benchmarks, indicating that the proposed descriptor is suited to represent pedestrian behaviors.

Demo Video

Motivation

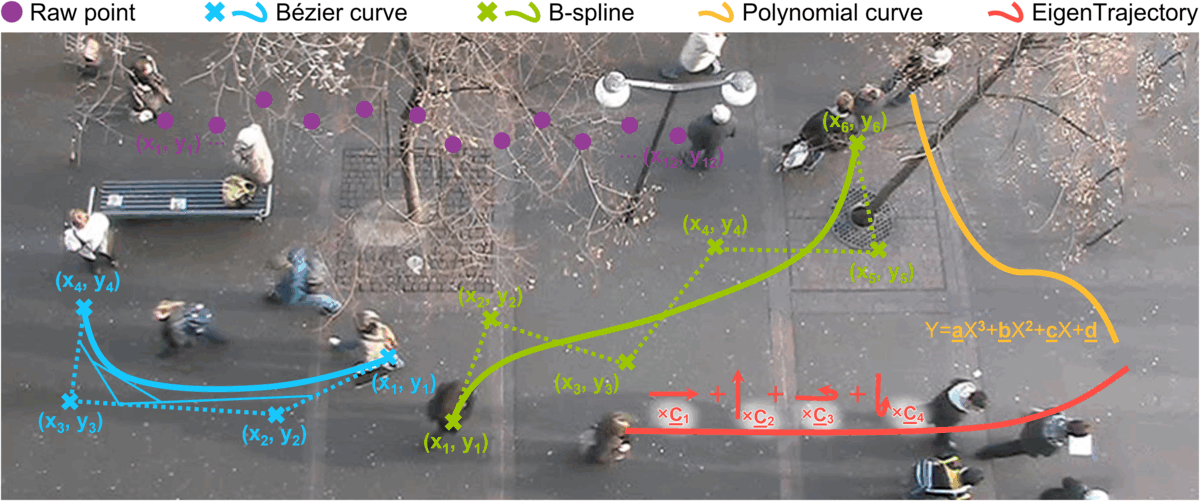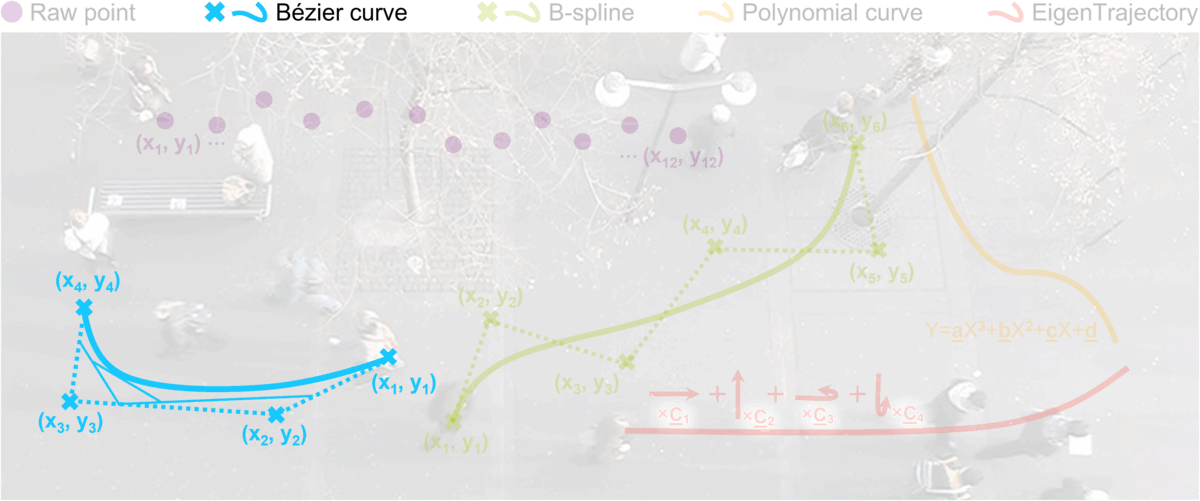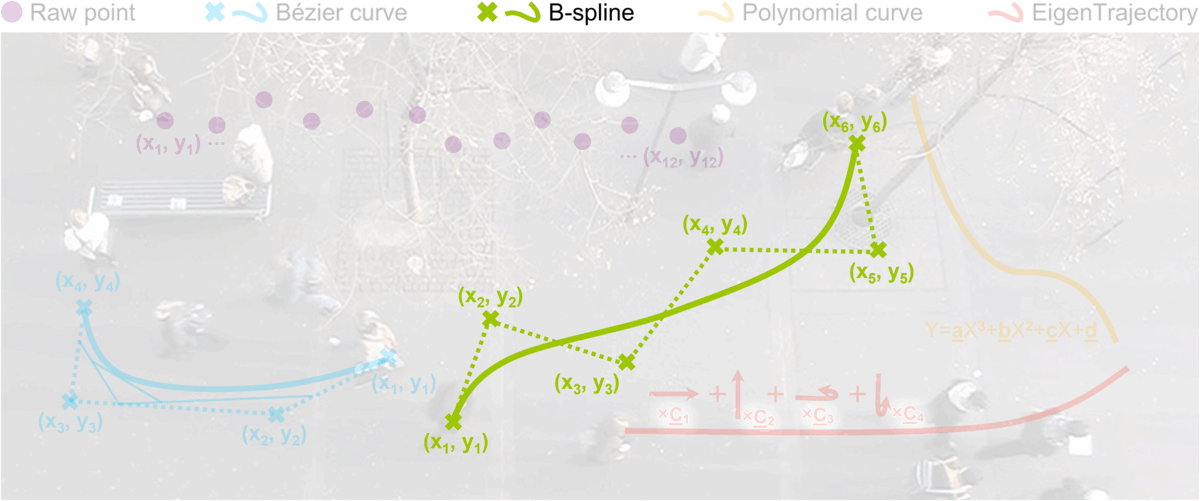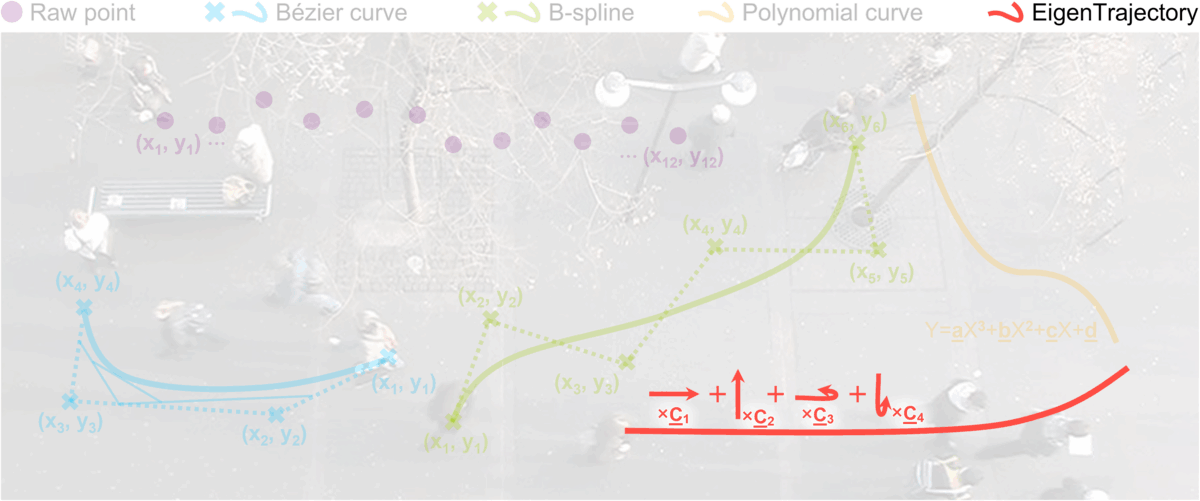
Prediction From Raw Trajectory Data

Many existing approaches design their prediction models in the Euclidean space, i.e., to directly infer a sequence of 2D coordinates of future frames. These approaches force the models to learn both informative behavioral features and their motion dynamics from raw trajectory data. Such direct predictions can intuitively describe agents' behaviors in the temporal series of spatial coordinates; however, in a higher-dimensional space, it is hard for the models to determine explanatory features.

Prediction Using Parametric Curve

Recent works have described the pedestrian's movements using trajectory descriptors instead of dealing with all raw coordinate information. Inspired by human beings traveling pathways with a higher level of connotation (e.g., a person who gradually decelerates to turn right, or makes a sharp turn while going straight), parametric curve functions (e.g., Bézier curve or B-spline curve) are introduced. These methods successfully reduce the dimensionality of trajectories by abstractly representing lengthy sequential coordinates in a spatial domain using a smaller set of key points. It is, however, unclear how well these parametric functions can capture human motions and behaviors as they have been designed for computer graphics and part modeling.

🌌 EigenTrajectory (𝔼𝕋) 🌌

EigenTrajectory (𝔼𝕋) Space

In this paper, departing from existing parametric curve functions, we present an intuitive trajectory descriptor that is learnable from real-world human trajectory data. First, we decompose a stacked trajectory sequence using Singular Value Decomposition (SVD). To represent the data concisely, we reduce the dimensionality by performing the best rank-k approximation. Through this process, all trajectories can be approximated as a linear combination of k eigenvectors, which we call EigenTrajectory (𝔼𝕋) descriptor. Next, we aggregate the social interaction features and then predict the coefficients of the eigenvectors for the future path in the same space. Here, after clustering the coefficients, a set of trajectory anchors, which can be interpreted as the coefficient candidates, is used to ensure a diversity of prediction paths. Finally, trajectory coordinates can be reconstructed through the matrix multiplication of the eigenvector and the coefficients.

𝔼𝕋 Descriptor

We assume that pedestrian movements are mainly represented by directions and speed variations that can be captured via principal components in the data. Since a little noise from people's staggering or tracking can also be added into the representation, we assume that using the top k components in the eigenvectors would be sufficient to correspond to the raw trajectory data. To fully benefit from the successful dimensionality reduction of SVD, we also apply it into our framework to represent spatio-temporal trajectory data as a linear combination of a set of eigenvectors. The proposed 𝔼𝕋 descriptor consists of two elements: k most representative singular vectors of trajectories and their combination coefficients that can explain any given trajectory.

Forecasting in the 𝔼𝕋 Space

Using the 𝔼𝕋 descriptor and transformation operators, we optimize each module designed for trajectory forecasting in our 𝔼𝕋 space (observed trajectory projection, history encoder, interaction modeling, extrapolation decoder, and predicted trajectory reconstruction modules). In addition, we propose a trajectory anchor to ensure the diversity of the predicted trajectories (trajectory anchor generation stage). This enables the off-the-shelf forecasting model to take the full benefits of the 𝔼𝕋 descriptor in an end-to-end manner.

Qualitative Results

BibTeX

@inproceedings{bae2023eigentrajectory,
  title={EigenTrajectory: Low-Rank Descriptors for Multi-Modal Trajectory Forecasting},
  author={Bae, Inhwan and Oh, Jean and Jeon, Hae-Gon},
  booktitle={Proceedings of the IEEE/CVF International Conference on Computer Vision},
  year={2023}
}